Mean Squared Error (MSE) in Machine Learning

When building machine learning models, evaluating their performance is crucial to ensure they provide accurate predictions. One of the most commonly used metrics for this purpose is the Mean Squared Error (MSE).

In this article, we’ll explore what MSE is, how it works, and why it’s so important in machine learning.

What is Mean Squared Error?

Mean Squared Error (MSE) is a measure of how close a model’s predictions are to the actual values. In simpler terms, it tells you how “off” your model’s guesses are on average.

Formula :

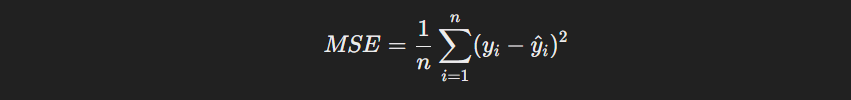
To simplify the formula, here is the breakdown:

• Calculate the difference: For each data point, subtract the predicted value from the actual value.
• Square the differences: This ensures all differences are positive, regardless of whether the prediction was too high or too low.
• Average the squared differences: This gives you the mean squared error.

Why do we square the differences?

• Positive values: Squaring ensures all differences are positive, making it easier to compare them.
• Weighting large errors: Squaring also gives more weight to larger errors, which can be important in some applications.

A lower MSE is better. A model with a lower MSE means its predictions are closer to the actual values, indicating a better fit to the data.

Imagine you’re trying to predict the height of a tree based on its age.

Age (years)	Actual Height (feet)	Predicted Height (feet)
5	20	18
10	35	30
15	45	42

Calculating the MSE:

Find the difference between the actual and predicted heights:

1. For the first tree: 20 – 18 = 2
2. For the second tree: 35 – 30 = 5
3. For the third tree: 45 – 42 = 3

Square the differences:

• 2^2 = 4
• 5^2 = 25
• 3^2 = 9

Calculate the average of the squared differences:

(4 + 25 + 9) / 3 = 12.67

So, the MSE for this prediction model is 12.67 square feet. This indicates that, on average, the model’s predictions are off by about 12.67 square feet. This means the predictions are closer to the actual values.

Importance of MSE in Machine Learning

MSE is widely used in machine learning for several reasons:

1. Interpretability: MSE clearly indicates how well a model is performing. A lower MSE value indicates better model performance, meaning the predicted values are closer to the actual values.
2. Model Optimization: Many machine learning algorithms, such as linear regression and neural networks, use MSE as a loss function during training. The goal is to minimize the MSE, which helps the model make more accurate predictions.

MSE in Linear Regression

Consider a simple linear regression model predicting house prices based on square footage. After training the model, you compare the predicted prices with the actual prices of houses in a test dataset. If the predicted prices are close to the actual prices, the MSE will be low, indicating that your model is performing well.

For instance, if the actual house prices are £200,000, £300,000, and £400,000, and the model predicts £210,000, £290,000, and £390,000, the MSE would be 100,000,000.

It indicates that the model is slightly off, and further optimization might be necessary.

Drawbacks of Mean Squared Error (MSE)

While MSE is a widely used metric, it has some drawbacks that should be considered:

1. Sensitivity to Outliers: MSE gives more weight to larger errors due to the squaring operation. This can be problematic when dealing with datasets containing outliers, as these extreme values can significantly influence the overall MSE.
2. Assumption of Normality: MSE assumes that the errors are normally distributed. If this assumption is violated, the MSE may not accurately reflect the model’s performance.
3. Lack of Interpretability: The units of MSE are squared units of the target variable. This can make it difficult to interpret the results in a meaningful way, especially for non-experts.
4. Non-Robustness: MSE is not robust to changes in the data distribution. Small changes in the data can lead to significant changes in the MSE.